The “now-focusing effect” inevitably leads to a preference for spending over saving.
But can we even process economic numbers correctly?

Sri Humana: So, what shall we discuss today?
Ann: I heard an interesting news story; it said our per-capita income is actually growing.
Garret: Boring. I watched a fascinating horror movie instead.
Sarah: Emily has nightmares, and I can’t sleep all night.
Thomas: To tell you the truth, I do not like horror movies. But judging from the ones I have seen, the whole script usually revolves around some kind of a monster. These horrible creatures rarely have much in common; they’re rather unique. But how about this: suppose someone combined the Predator, the Alien, Godzilla, Dracula and Jason into one “average monster.” What would it look like? I think it would be funny and bizarre.
Now, in your everyday life, you are bombarded with all kinds of average statistics. Journalists use them, politicians use them and your boss uses them.
Average salary, average IQ, average results and of course the average person. The average person on Earth is 1.8 meters tall, has a 110 IQ, earns $5000 per year, has one and a half children, is half Chinese and half Indian, and half man half woman. What a monster!!!
The most dangerous average monsters are the ones in areas where results or outcomes are not equally distributed. Areas like wealth, internet traffic, city sizes, areas destroyed by fire and all sorts of other social phenomena.
Don’t get me wrong, averages do have some meaning and use, but mostly when they’re mentioned in connection with things that are distributed normally. Things like people’s height, health, and school grades. Or the number of sunny days in a year, etc.
For example, consider the average wealth of a random, relatively small group of people. Now add Bill Gates to that same group, and calculate the average again. What happens to the average figure?
Now consider the average IQ of a similar random group. Then add Einstein to the group, and calculate again. How would the average IQ change?
There is a useful tool for measuring variability, but remember it is useful only if your data is distributed normally – for example, the way body part sizes appear among a group of people, with all values falling within a fairly well-defined range. This tool is the metric known as standard deviation. It simply measures how far a particular measurement is found to deviate from the average (mean) measurement, in a particular group. A low standard deviation means that the data points tend to be very close to the mean. A high standard deviation means that the data points are spread over a large range of values, some far from the mean. (If you calculate the standard deviation in a group to be very high, it may mean your average figure is of little or no use.)
Now, don’t worry – we’ll get to how you can use this tool in managing your wealth very soon. First, we’ll look at how to calculate it – then we can put it to work.
Stop believing in “average monsters” and your nightmares might go away.
For the sake of example, let’s imagine you have a small flock of seven chickens, and you sell their eggs (yes, “nest eggs”). You want to find out the average number of eggs each chicken lays each year, and how much variation there is within the group (the standard deviation). You have kept a record of each chicken’s production for the past year, and you are ready to do the math.
Here are the eight steps for calculating standard deviation:
- Organize your data – gather it all together so you can work with it. In this case, get out your record of each chicken’s production.
- Add your data. Find the total number of eggs your whole flock chickens produced. We’ll say it was 980 eggs.
- Calculate the average of your data by dividing the total by the number (count) of records (the number of chickens for which you kept records: 7) This gives you 980/7=140. That means the average number of eggs per chicken was 140.
- Subtract the average number from each record. For example, if Chicken #1 (Betsy) laid 120 eggs, you would subtract 140 from 120. Write that number down, and then go through the same process for the other six chickens.
- Square the above numbers. That is, multiply each of the numbers you found by itself. Betsy’s number would be 20 x 20, or 400. Write that down and repeat the process for the rest of the flock’s numbers from step 4.
- Add up all the squared numbers.
- Calculate the average of all the numbers found in step 5.
- Calculate the square root of the number you found in step 7. The number you find here is the standard deviation.
*NOTE: There IS a shorter and easier way to do this, if you happen to have a spreadsheet app such as MS Excel, and know how to use it. Just create a spreadsheet for your data and use the STDEV function.
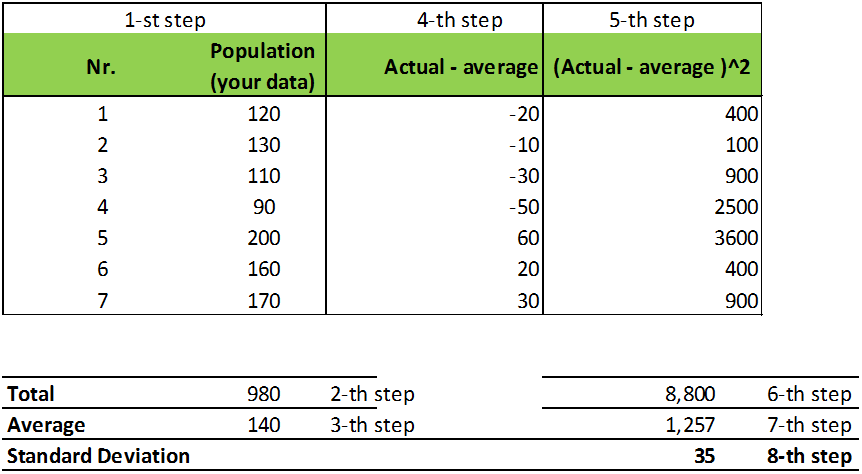
In this example, 35 is your standard deviation. That means you can anticipate that if you add a chicken to your flock, you will end up with 140 more eggs in the next year, plus or minus 35 eggs. (That is, you might get as few as 105 or as many as 175, but it’s likely to be closer to 140.) This also assumes that your sample (the records for your seven chickens) is representative of all chickens in the region.
Standard deviation is a widely used metric, especially for evaluating risks. Be careful in using it, though – many people fall into a trap when using standard deviation: they become overconfident about risks in domains which have extreme distributions. (This common mistake actually contributed to the financial crisis of 2008.) So, use standard deviation wisely, and don’t get overconfident about it – especially when using it in the social domain.
Some questions for you:
- Do you consider yourself an average person?
- What is the average day temperature in the Sahara? In Chicago?